In electronics terms, a flip flop means a circuit that contains two stable states. These stable states can be used to store binary data (also known as base two system data).
These stable states take inputs and produce output according to them. When we talk about overall digital program fragmentation, “Flip flops and latches” are its foundation. They both are used in making various communication, computers and other system programs as data storage elements.
About Binary
Before moving ahead, we should know about “binary” first because it is the foundation process we should learn before understanding the workings of flip flops and latches.
Binary is a numeric system that uses only two digits: 0 and 1. So that’s why
people also termed it as a base two system. Every signal which a computer gets from a processor, gets in binary language, it is the only machine language which computer and other devices recognize. So all programs which you see on a computer are represented by it.
We can convert each and every numeric or alphabet character into a binary term. For this, we need to clearly understand its process:
In case of numeric values:
Normal numeric values are written in the base 10 system, In the base 10 system, we use 10 digits, i.e., 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, to represent any numeric value.
But in the binary system, as we already mentioned, only two digits, 0 and 1, are required in the formation of any value.
To convert any base 10 system value into binary terms, the system needs to follow a conversion process, in which each value is divided by 2 until the remainder becomes 1.
For example:
If we need to convert 178 into binary format following process shall be followed:
| Calculation | Remainder |
| 178/2= 84 | 0 |
| 84/2= 42 | 0 |
| 42/2= 21 | 0 |
| 21/2= 10 | 1 |
| 10/2= 5 | 0 |
| 5/2= 2 | 1 |
| 2/2= 1 | 0 |
Now, we need to write 1 in starting and then arrange the remainder in from bottom to top level to get the binary number of any decimal value.
For numeric value 178, the binary number is 10101000.
In case of text;
While translating any text into the binary term, we will require knowledge of ASCII (American standard code for information interchange). We will not discuss this table in detail in the current blog because it is not our main subject.
This is an ASCII table to calculate the binary value for alphabets. To convert them, we just need to translate ASCII numeric code into binary numbers by following the same process which was mentioned for numeric values.
Early Development of Flip Flops
The first electronic flip-flop was developed by British physicists William Eccles and F.W. Jordan in the year 1918. Initially, they named it the “Eccles-Jordan trigger circuit”.
In 1943, this design was used in the making of the Colossus codebreaking computer. Even after the introduction of integrated circuits, they are still relevant.
According to US Jet Propulsion Laboratory’s engineer P.L. Lindley, the flip-flop types, i.e., SR, D, JK, T, were initially discussed in a UCLA computer course designed by Montgomery Phister in the year 1954 and then it also gets published in “Logical design of digital” book.
Basic difference between Flip flops and latches
To understand the basic difference between Flip flop and latch, first we need to know about latch.
What is latch?
The latch is an electronic logic circuit that works on a “Bistable Multivibrator,” It operates on two stable states, i.e., High output and low output. Basically, a latch can be termed a data storage device, i.e., a memory device, which stores data for a limited time period, i.e., till the device is powered on.
Latches are input-sensitive. Unlike flip flops, they are levelly triggered, instead of working on the basis of edges of the clock system.
What is flip flop?
Flip flop contains a couple of latches. Instead of one, they have two outputs and two inputs, i.e., one for set and another for reset. Their main use is to save binary data. The main difference is the extra CLK (Clock) signal, and it works like a metronome that coordinates the digital circuit’s actions.
Although, they consume more power and time to work than laches.
Imposition of Flip flops
Flip flops can be made in two ways, i.e., simple (asynchronous) and clocked (synchronous). As stated above, simple ones are known as latches, while clocked ones are known as flops.
Since it is used as a data storage element, its imposition requires various other elements like vacuum tubes, Field effects, inverters, bipolar transistors, etc. All these items will probably be required in its implementation. Still, special devices like synchronous systems will be required for clocked devices.
Types of Flip flops
Flip flops broadly can be categorized into four categories, i.e., SR, D, T, JK. Each type’s work process depends on its equation and characteristics. For example, the workflow and data storage system mainly depend on clock pulse.
Each type of flip flop further described as follows:
SR (Set-reset flip flop)
In electronic terms, SR denotes set and reset, S for set and R for reset. It is the simplest variant of Flip flop that is easy to understand and implement. Most commonly, programmers take this variant as a base for their program.
| Clock | S | R | Q | Qn+1 |
| ^ | 0 | 0 | No change | 1 |
| ^ | 0 | 1 | No change | 1 |
| ^ | 1 | 0 | 1 | 0 |
| ^ | 1 | 1 | Invalid | Invalid |
In SR, Flip flops, S and R denote input, Q means current output, and Qn+1 denotes future outcome. When set and reset inputs, i.e., S and R, are low, present and future outcome doesn’t change, in equation format, S=R=0 then Q = Qn+1.
While S is high and R is low, it will force Q to remain high until; S (set) returns to normal low, i.e., Set=1 and R=0, then Q will be forced high =1 and Qn+1 = 0.
Following other equations can be made with the help of the truth table.
Electric students can now easily prepare a transition table based on the above data.
D Flip Flop
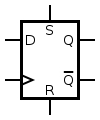
Data or delay flip flop model is another flip flop variant which is used by programmers frequently.
|
Inputs |
Output |
||||
|
S |
R |
D |
> |
Q |
QN+1 |
|
0 |
1 |
IRRELEVANT |
0 |
1 |
|
|
1 |
0 |
1 |
0 |
||
|
1 |
1 |
1 |
1 |
||
A Truth table for D flip flop model
Here D denotes the substantial input portion of the clock cycle, and it does not change.
As we can see in the picture, the d flip flop can be termed as a modification of the Set-reset model. The value of output in this model only changes when the clock’s edge is in a rising position. Otherwise, it will be unaffected.
In this model, the popular equation S=R=1 can be resolved, and it becomes S=R=0, and its behavior in other conditions can be traced from the above Truth table of D flip flop.
The D flip flop is very useful in making many electronic base devices because they play a crucial role in making shift registers.
The shift register is one kind of digital circuit (digital model of computation) that makes the output of one flip flop to the input of another flip flop.
It gives you an advantage that its input captures the clocked moment of the flip flop and changes only when the next clock moment hits. Otherwise, it will ignore all other inputs.
However, there might be an option for reset signal input, which can make present input 0, i.e., reset Q to 0, parallel or not, according to the clock.
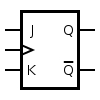
JK Flip flop
JK flip flop also modifies the SR flip flop, i.e., J represents set and K represents reset. Its equitation can be termed as J=K=1. In the JK flip flop, inputs J and K work like inputs S and R to set and reset for the flip flop program.
|
JK Flip flop Truth Table |
||||||||
|
Characteristic table |
Excitation table |
|||||||
|
J |
K |
Remarks |
Qn+1 |
Q |
Qn+1 |
Remarks |
J |
K |
|
0 |
0 |
Hold |
Q |
0 |
1 |
No change |
0 |
Irrelevant |
|
0 |
1 |
Reset |
0 |
0 |
1 |
Set |
1 |
|
|
1 |
0 |
Set |
1 |
1 |
0 |
Reset |
Irrelevant |
1 |
|
1 |
1 |
Toggle |
– |
1 |
1 |
No change |
0 |
|
According to this model: inputs refer to J and K, and the outcome responses according to them, i.e., in the first situation both J and K remain at a low level, then no change will occur, according to the second situation, if J at a high level and K at a lower level, the outcome will enhance the value of J till next clock edge. On the contrary, if input J is low and input K is high, it will set this situation.
There are also other equations that you can see in the truth table.
T Flip flop
T flip flop can be said as another version of JK flip flop. It is a single input version of the JK flip flop, whereas, in the JK flip flop, we get two inputs, J and K, while there is only one input, i.e., T input.
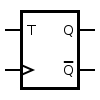
It combines the operation of both J and K inputs in a single input called T, basically it toggles the output. You can see its various equation in the T flip flop truth table given below:
Considering the above table, we can summarize that when input T is Low, the flip flop holds its value. But, on the other hand, when the value of T input is high, it changes the value of the T flip flop, i.e., toggle it.
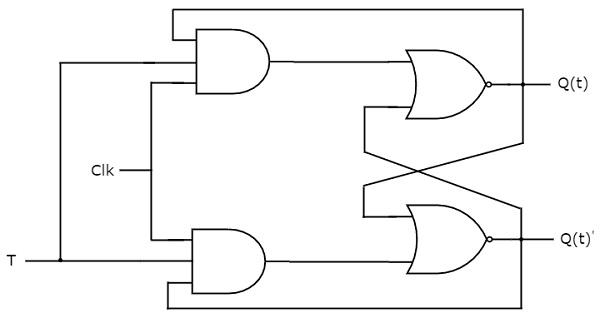
Flip flop applications:
All flip flops which were discussed above has a very wide usage in digital electronics development, for instance:
- Data storage
- Frequency division
- Bounce elimination switch
These are some examples of Flip flops applications.
Other related terms:
Timing parameters: timing of input holding is very important to perform a flip flop effectively. We can understand this term by the following example, imagine a horse is running and if you want to take a picture of that horse, so you have to wait till the horse stop running; otherwise, your picture will become blurry, in another case, if you take photos of the horse while it was standing, you will get a clear picture.
The same example we can apply on the flip flop; means the input for the flip flop should be held steady during its aperture. Otherwise, we will not get a desirable result.
Setup time: The input data’s minimum holding time so that the clock can reliably sample it, it is called setup time. It shall be held till the occurrence of the clock event.
Aperture: Aperture is the combination of setup and hold time, the system needs to hold input till aperture time to get effective results.
Hold time: it is the time period for which input shall be held after the occurrence of a clock event.
Recovery time: It is the minimum requisite time in which asynchronous inputs, i.e. both set and reset. Should be inactive steadily till occurrence of clock event, so that clock can reliably sample the input data. It is similar to setup time.
Removal time: It is similar to hold time period, it can be defined as the minimum required time for which asynchronous inputs i.e. both set and reset. Should be held after the occurrence of a clock event.
What is metastability?
Metastability refers to a pervasive problem of flip flops, it relates to the situation where two inputs change simultaneously, i.e., clock and reset or clock and data. However, this situation does not always create a problem.
it can cause an unpredictable output when the program order is unclear. Also, this type of outcome can take a much longer time than a normal one to change its state. Although, the normal time is not specific, it is subjective.
When we talk about a computer system as a whole, it can also interrupt the program flow when another circuit uses its value before rectifying it, i.e., unstable value.
However, the metastability problem can be avoided by developing adequate controls and clearly setting inputs for setup and holding time to avoid confusion.
Let’s talk about perfectly metastability error-free flip flops. It is practically impossible because most flip-flops are connected through real-time signals. Even a nanosecond time difference can create a problem that leads to metastability.
However, we can significantly reduce its risk by applying effective setup and hold time inputs. We can also make a chain of flip flops that uses the output of one process as the input of the upcoming flip flop.
We can reduce its risk by doing safety measures, although it might not be possible to finish it.
Conclusion
After reading the above article, we hope that you get what you were looking for about flip flops. If you have any query about our content, let us know in the comment section, we will try our best to answer you asap.























